以平滑判据，即地表发射率光谱比大气下行辐射光谱平滑，发展的一类高光谱温度与发射率分离算法，会因发射率计算在数值上的不稳定而失效,即产生远大于1或远小于0的发射率(定义为奇异发射率)。例如在光谱迭代平滑算法（ISSTES）里面，奇异发射率会导致平滑度变得很大（图1），将其对应的温度标识为不准确，无视其实际情况(Cheng et al.,2008)。

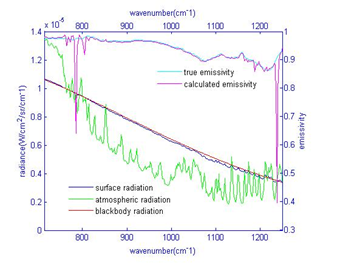
图1 计算的发射率和真实发射率以及用来计算发射率的各个辐亮度的比较

换一个思路，寻求发展不会因产生发射率奇异值导致的算法失效的新算法。

针对高光谱热红外数据（~1cm^-1）而言，在相对窄的光谱区间（例如小于15cm^-1），普朗克函数可以近似为波数的线性函数，地表自身的辐射也可以近似为波数的线性函数，大气的下行辐射含有尖锐的大气发射线，表现出强烈的光谱反差。假设地表温度为300K，地表发射率为常数0.85。大气下行辐射使用MODTRAN 4.0模拟，采用的大气模式为1976 US Standard Atmosphere。

给定大气强发射线位置的发射率初值，假设窄光谱区间发射率为常数，可以计算出地表自身辐射。如果发射率初值等于真值，计算的地表自身辐射不含有大气下行辐射残留。否则，计算的地表自身辐射将含有明显的大气下行辐射残留。直线距离BD来刻画残留程度，B是大气吸收线的位置，D为直线AC上的点，他的横坐标与B同。如果发射率初值是最合适的，他对应残差将是最小的。采用逐步求精的方法确定大气发射线处的地表发射率，然后由相应的传感器辐射测量计算地表温度以及地表发射率光谱。

该方法可以有效避免平滑算法的奇异发射率问题，获得精度较高的地表发射率光谱。

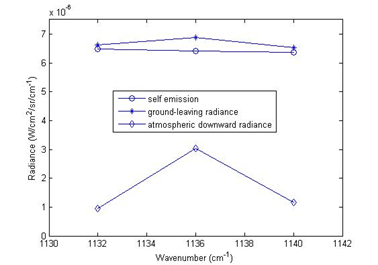
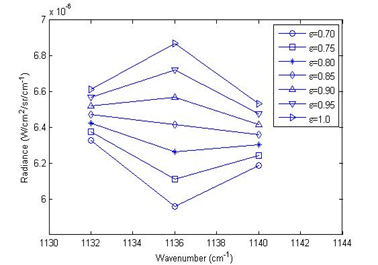
(a)                                                                                        (b)

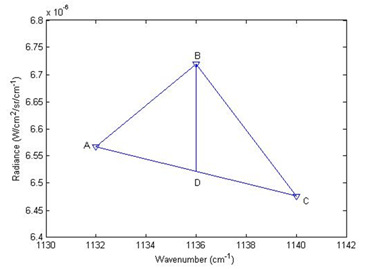
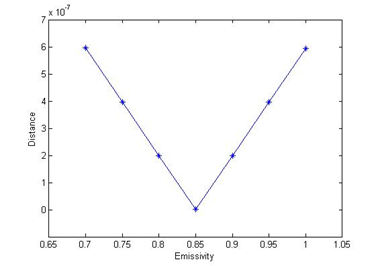
(c)                                                                                        (d)

图2 逐步求精算法示意图

参考文献：

1. Cheng, J., Liang, S., Wang, J., & Li, X. (2010). A Stepwise Refining Algorithm of Temperature and Emissivity Separation for Hyperspectral Thermal Infrared Data. IEEE Transactions on Geoscience and Remote Sensing, 48, 1588-1597（下载）

2. Cheng, J., Liang, S., Liu, Q., & Li, X. (2011). Temperature and emissivity separation from ground-based MIR hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing, 49, 1473-1484 （下载）